Scientific Programming with NumPy
Overview
Teaching: 60 min
Exercises: 20 minQuestions
What are the differences between NumPy arrays and Python lists?
How do I extract subsets of data from a dataset?
How can I use NumPy to tell me basic statistical properties about my data?
Objectives
Explain the key similarities and differences between NumPy arrays and Python lists.
Select subsets of data from a NumPy array using Python slicing.
Efficiently perform elementwise operations on data.
Obtain basic characteristics of tabular data using NumPy’s statistical functions.
Apply operations to differently sized arrays.
Introduction to NumPy
See slides at slides.
NumPy Arrays vs Python Lists
NumPy’s array type represents a multidimensional matrix Mi,j,k…n
The NumPy array seems at first to be just like a list:
import numpy as np
my_array = np.array(range(5))
my_array
Note here we are importing the NumPy module as np, an established convention for using NumPy which means we can refer to NumPy using np. instead of the slightly more laborious numpy..
array([0, 1, 2, 3, 4])
Ok, so they look like a list.
my_array[2]
2
We can access them like a list.
We can also access NumPy arrays as a collection in for loops:
for element in my_array:
print("Hello" * element)
Hello
HelloHello
HelloHelloHello
HelloHelloHelloHello
However, we can also see our first weakness of NumPy arrays versus Python lists:
my_array.append(4)
---
AttributeError Traceback (most recent call last)
<ipython-input-10-b12177763178> in <module>()
----> 1 my_array.append(4)
AttributeError: 'numpy.ndarray' object has no attribute 'append'
For NumPy arrays, you typically don’t change the data size once you’ve defined your array, whereas for Python lists, you can do this efficiently. Also, NumPy arrays only contain one datatype. However, you get back lots of goodies in return…
Elementwise Operations
One great advantage of NumPy arrays is that most operations can be applied element-wise automatically, and in a very Pythonic way!
my_array + 2
+ in this context is an elementwise operation performed on all the matrix elements.
array([2, 3, 4, 5, 6])
These are known as ‘vectorised’ operations, and are very fast. We’ll be looking at making use of these in more detail next week when we look at optimisation.
But for now, let’s take a brief look at a basic example that demonstrates the performance of NumPy over Python lists. First, using Python lists we can do the following, that creates a 2D list of size 10000x10000, sets all elements to zero, then adds 10 to all those elements:
%%timeit
nested_list = [[0 for _ in range(10000)] for _ in range(10000)]
nested_list = [[x+10 for x in column] for column in nested_list]
Here, we use %timeit magic to run this cell a number of times and display an average time for how long it took to run. More information on timeit is available.
That took a while! In NumPy we replicate this by doing:
%%timeit
import numpy as np
array = np.zeros((10000, 10000))
array = array + 10
Here, we import the NumPy library, use a specialised function to set up a NumPy array of size 10000x10000 with elements set to zero, and then - in a very Pythonic way - add 10 to each element. It’s simpler, closer to our conceptual model of what we want to achieve, and it’s much faster.
Revisiting our Inflammation Dataset
Let’s take a more in-depth look at our CSV inflammation dataset we looked at previously.
As before, we can use NumPy to load our dataset into a Python variable:
data = np.loadtxt(fname='../data/inflammation-01.csv', delimiter=',')
data
array([[0., 0., 1., ..., 3., 0., 0.],
[0., 1., 2., ..., 1., 0., 1.],
[0., 1., 1., ..., 2., 1., 1.],
...,
[0., 1., 1., ..., 1., 1., 1.],
[0., 0., 0., ..., 0., 2., 0.],
[0., 0., 1., ..., 1., 1., 0.]])
As a reminder, each row holds information for a single patient, and the columns represent successive days. Each value represents a single inflammation reading for a patient.
In the Corner
What may also surprise you is that when Python displays an array, it shows the element with index
[0, 0]in the upper left corner rather than the lower left. This is consistent with the way mathematicians draw matrices but different from the Cartesian coordinates. The indices are (row, column) instead of (column, row) for the same reason, which can be confusing when plotting data.
Examining our Dataset
Let’s ask what type of thing data refers to:
print(type(data))
<class 'numpy.ndarray'>
The output tells us that data currently refers to an N-dimensional array, the functionality for which is provided by the NumPy library.
Data Type
A Numpy array contains one or more elements of the same type. The
typefunction will only tell you that a variable is a NumPy array but won’t tell you the type of thing inside the array. We can find out the type of the data contained in the NumPy array.print(data.dtype)dtype('float64')This tells us that the NumPy array’s elements are floating-point numbers.
With the following command, we can see the array’s shape:
print(data.shape)
(60, 40)
The output tells us that the data array variable contains 60 rows and 40 columns, as we would expect.
We can also access specific elements of our 2D array (such as the first value) like this:
data[0, 0]
0.0
Or the value in the middle of the dataset:
data[30, 20]
13.0
Slicing our Inflammation Data
An index like [30, 20] selects a single element of an array, but similar to how we slice lists, we can slice whole sections of NumPy arrays as well.
For example, we can select the first ten days (columns) of values for the first four patients (rows) like this:
data[0:4, 0:10]
[[ 0. 0. 1. 3. 1. 2. 4. 7. 8. 3.]
[ 0. 1. 2. 1. 2. 1. 3. 2. 2. 6.]
[ 0. 1. 1. 3. 3. 2. 6. 2. 5. 9.]
[ 0. 0. 2. 0. 4. 2. 2. 1. 6. 7.]]
So here 0:4 means, “Start at index 0 and go up to, but not including, index 4.” Again, the up-to-but-not-including takes a bit of getting used to, but the rule is that the difference between the upper and lower bounds is the number of values in the slice.
And as we saw with lists, we don’t have to start slices at 0:
data[5:10, 0:10]
Which will show us data from patients 5-9 (rows) across the first 10 days (columns):
[[ 0. 0. 1. 2. 2. 4. 2. 1. 6. 4.]
[ 0. 0. 2. 2. 4. 2. 2. 5. 5. 8.]
[ 0. 0. 1. 2. 3. 1. 2. 3. 5. 3.]
[ 0. 0. 0. 3. 1. 5. 6. 5. 5. 8.]
[ 0. 1. 1. 2. 1. 3. 5. 3. 5. 8.]]
We also don’t have to include the upper and lower bound on the slice. If we don’t include the lower bound, Python uses 0 by default; if we don’t include the upper, the slice runs to the end of the axis, and if we don’t include either (i.e., if we just use ‘:’ on its own), the slice includes everything:
small = data[:3, 36:]
small
The above example selects rows 0 through 2 and columns 36 through to the end of the array:
[[ 2. 3. 0. 0.]
[ 1. 1. 0. 1.]
[ 2. 2. 1. 1.]]
Numpy Memory
Numpy memory management can be tricksy:
x = np.arange(5) y = x[:]y[2] = 0 xarray([0, 1, 0, 3, 4])It does not behave like lists!
x = list(range(5)) y = x[:]y[2] = 0 x[0, 1, 2, 3, 4]We must use np.copy to force separate memory. Otherwise NumPy tries its hardest to make slices be views on data.
Elementwise Operations on Multiple Arrays
As we’ve seen, arrays also know how to perform common mathematical operations on their values element-by-element:
doubledata = data * 2.0
Will create a new array doubledata, each element of which is twice the value of the corresponding element in data:
print('original:')
data[:3, 36:]
print('doubledata:')
doubledata[:3, 36:]
original:
[[ 2. 3. 0. 0.]
[ 1. 1. 0. 1.]
[ 2. 2. 1. 1.]]
doubledata:
[[ 4. 6. 0. 0.]
[ 2. 2. 0. 2.]
[ 4. 4. 2. 2.]]
If, instead of taking an array and doing arithmetic with a single value (as above), you did the arithmetic operation with another array of the same shape, the operation will be done on corresponding elements of the two arrays:
tripledata = doubledata + data
Will give you an array where tripledata[0,0] will equal doubledata[0,0] plus data[0,0],
and so on for all other elements of the arrays.
print('tripledata:')
print(tripledata[:3, 36:])
tripledata:
[[ 6. 9. 0. 0.]
[ 3. 3. 0. 3.]
[ 6. 6. 3. 3.]]
Stacking Arrays
Arrays can be concatenated and stacked on top of one another, using NumPy’s
vstackandhstackfunctions for vertical and horizontal stacking, respectively.import numpy A = np.array([[1,2,3], [4,5,6], [7,8,9]]) print('A = ') print(A) B = np.hstack([A, A]) print('B = ') print(B) C = np.vstack([A, A]) print('C = ') print(C)A = [[1 2 3] [4 5 6] [7 8 9]] B = [[1 2 3 1 2 3] [4 5 6 4 5 6] [7 8 9 7 8 9]] C = [[1 2 3] [4 5 6] [7 8 9] [1 2 3] [4 5 6] [7 8 9]]Write some additional code that slices the first and last columns of our inflammation
dataarray, and stacks them into a 60x2 array, to give us data from the first and last days of our trial across all patients. Make sure toSolution
A ‘gotcha’ with array indexing is that singleton dimensions are dropped by default. That means
data[:, 0]is a one dimensional array, which won’t stack as desired. To preserve singleton dimensions, the index itself can be a slice or array. For example,data[:, :1]returns a two dimensional array with one singleton dimension (i.e. a column vector).D = np.hstack([data[:, :1], data[:, -1:]]) print('D = ') print(D)D = [[0. 0.] [0. 1.] ... [0. 0.] [0. 0.]]
Dot Products
You can also do dot products of NumPy arrays:
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
np.dot(a, b)
array([[19, 22],
[43, 50]])
More Complex Operations
Often, we want to do more than add, subtract, multiply, and divide array elements. NumPy knows how to do more complex operations, too. If we want to find the average inflammation for all patients on all days, for example, we can ask NumPy to compute data’s mean value:
print(np.mean(data))
6.14875
mean is a function that takes an array as an argument.
Not All Functions Have Input
Generally, a function uses inputs to produce outputs. However, some functions produce outputs without needing any input. For example, checking the current time doesn’t require any input.
import time print(time.ctime())Sat Mar 26 13:07:33 2016For functions that don’t take in any arguments, we still need parentheses (
()) to tell Python to go and do something for us.
NumPy has lots of useful functions that take an array as input.
Let’s use three of those functions to get some descriptive values about the dataset. We’ll also use multiple assignment, a convenient Python feature that will enable us to do this all in one line.
maxval, minval, stdval = np.max(data), np.min(data), np.std(data)
print('max inflammation:', maxval)
print('min inflammation:', minval)
print('std deviation:', stdval)
Here we’ve assigned the return value from np.max(data) to the variable maxval, the value
from np.min(data) to minval, and so on.
max inflammation: 20.0
min inflammation: 0.0
std deviation: 4.61383319712
When analyzing data, though, we often want to look at variations in statistical values, such as the maximum inflammation per patient or the average inflammation per day. One way to do this is to create a new temporary array of the data we want, then ask it to do the calculation:
np.max(data[0, :])
So here, we’re looking at the maximum inflammation across all days for the first patient, which is
18.0
What if we need the maximum inflammation for each patient over all days (as in the next diagram on the left) or the average for each day (as in the diagram on the right)? As the diagram below shows, we want to perform the operation across an axis:
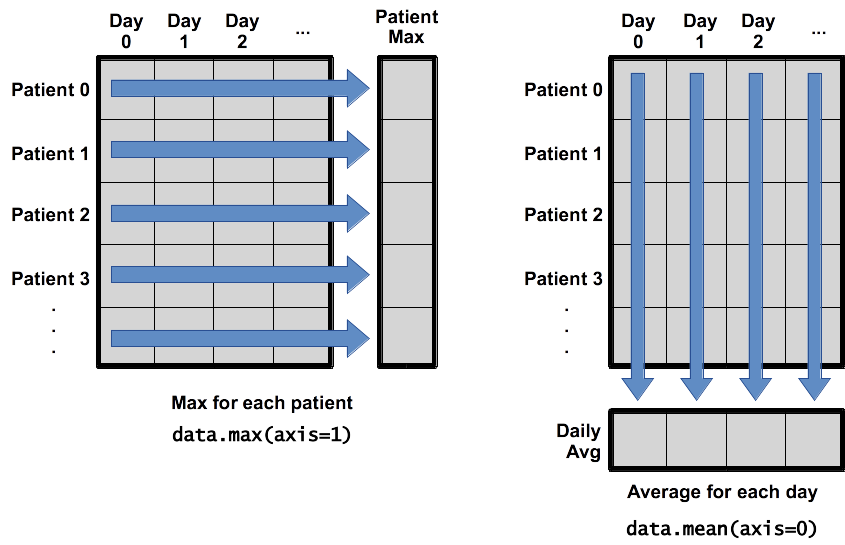
To support this functionality, most array functions allow us to specify the axis we want to work on. If we ask for the average across axis 0 (rows in our 2D example), we get:
print(np.mean(data, axis=0))
[ 0. 0.45 1.11666667 1.75 2.43333333 3.15
3.8 3.88333333 5.23333333 5.51666667 5.95 5.9
8.35 7.73333333 8.36666667 9.5 9.58333333
10.63333333 11.56666667 12.35 13.25 11.96666667
11.03333333 10.16666667 10. 8.66666667 9.15 7.25
7.33333333 6.58333333 6.06666667 5.95 5.11666667 3.6
3.3 3.56666667 2.48333333 1.5 1.13333333
0.56666667]
As a quick check, we can ask this array what its shape is:
print(np.mean(data, axis=0).shape)
(40,)
The expression (40,) tells us we have an N×1 vector, so this is the average inflammation per day for all patients. If we average across axis 1 (columns in our 2D example), we get:
patients_avg = np.mean(data, axis=1)
patients_avg
[ 5.45 5.425 6.1 5.9 5.55 6.225 5.975 6.65 6.625 6.525
6.775 5.8 6.225 5.75 5.225 6.3 6.55 5.7 5.85 6.55
5.775 5.825 6.175 6.1 5.8 6.425 6.05 6.025 6.175 6.55
6.175 6.35 6.725 6.125 7.075 5.725 5.925 6.15 6.075 5.75
5.975 5.725 6.3 5.9 6.75 5.925 7.225 6.15 5.95 6.275 5.7
6.1 6.825 5.975 6.725 5.7 6.25 6.4 7.05 5.9 ]
Which is the average inflammation per patient across all days.
Change In Inflammation
This patient data is longitudinal in the sense that each row represents a series of observations relating to one individual. This means that the change in inflammation over time is a meaningful concept.
The
np.diff()function takes a NumPy array and returns the differences between two successive values along a specified axis. For example, a NumPy array that looks like this:npdiff = np.array([ 0, 2, 5, 9, 14])Calling
np.diff(npdiff)would do the following calculations and put the answers in another array.[ 2 - 0, 5 - 2, 9 - 5, 14 - 9 ]np.diff(npdiff)array([2, 3, 4, 5])Which axis would it make sense to use this function along?
Solution
Since the row axis (0) is patients, it does not make sense to get the difference between two arbitrary patients. The column axis (1) is in days, so the difference is the change in inflammation – a meaningful concept.
np.diff(data, axis=1)If the shape of an individual data file is
(60, 40)(60 rows and 40 columns), what would the shape of the array be after you run thediff()function and why?Solution
The shape will be
(60, 39)because there is one fewer difference between columns than there are columns in the data.How would you find the largest change in inflammation for each patient? Does it matter if the change in inflammation is an increase or a decrease?
Solution
By using the
np.max()function after you apply thenp.diff()function, you will get the largest difference between days. We can functionally compose these together.np.max(np.diff(data, axis=1), axis=1)array([ 7., 12., 11., 10., 11., 13., 10., 8., 10., 10., 7., 7., 13., 7., 10., 10., 8., 10., 9., 10., 13., 7., 12., 9., 12., 11., 10., 10., 7., 10., 11., 10., 8., 11., 12., 10., 9., 10., 13., 10., 7., 7., 10., 13., 12., 8., 8., 10., 10., 9., 8., 13., 10., 7., 10., 8., 12., 10., 7., 12.])If inflammation values decrease along an axis, then the difference from one element to the next will be negative. If you are interested in the magnitude of the change and not the direction, the
np.absolute()function will provide that.Notice the difference if you get the largest absolute difference between readings.
np.max(np.absolute(np.diff(data, axis=1)), axis=1)array([ 12., 14., 11., 13., 11., 13., 10., 12., 10., 10., 10., 12., 13., 10., 11., 10., 12., 13., 9., 10., 13., 9., 12., 9., 12., 11., 10., 13., 9., 13., 11., 11., 8., 11., 12., 13., 9., 10., 13., 11., 11., 13., 11., 13., 13., 10., 9., 10., 10., 9., 9., 13., 10., 9., 10., 11., 13., 10., 10., 12.])
Multi-dimensional Arrays
NumPy’s true power comes from multi-dimensional arrays:
np.zeros([3, 4, 2]) # 3 arrays with 4 rows and 2 columns each
array([[[ 0., 0.],
[ 0., 0.],
[ 0., 0.],
[ 0., 0.]],
[[ 0., 0.],
[ 0., 0.],
[ 0., 0.],
[ 0., 0.]],
[[ 0., 0.],
[ 0., 0.],
[ 0., 0.],
[ 0., 0.]]])
Unlike a list-of-lists in Python, we can reshape arrays. Let’s split our inflammation dataset in half, so that our single 2-dimensional array of 60 patients over 40 days becomes an 3-dimensional array of two arrays of 30 patients over 40 days (essentially splitting the patients into two groups):
split_data = data.reshape(2, 30, 40)
split_data
By doing this, the original array data gets reshaped into the new array dimensions:
array([[[0., 0., 1., ..., 3., 0., 0.],
[0., 1., 2., ..., 1., 0., 1.],
[0., 1., 1., ..., 2., 1., 1.],
...,
[0., 0., 1., ..., 3., 2., 1.],
[0., 0., 2., ..., 3., 1., 0.],
[0., 0., 0., ..., 1., 0., 1.]],
[[0., 1., 1., ..., 3., 2., 1.],
[0., 0., 2., ..., 3., 0., 0.],
[0., 1., 2., ..., 0., 2., 1.],
...,
[0., 1., 1., ..., 1., 1., 1.],
[0., 0., 0., ..., 0., 2., 0.],
[0., 0., 1., ..., 1., 1., 0.]]])
And then, for example to get all inflammation data for the 10th patient in the first patient group:
split_data[0, 9]
array([ 0., 1., 2., 2., 4., 3., 1., 4., 8., 9., 5., 10., 10.,
3., 4., 6., 7., 11., 16., 6., 14., 9., 11., 10., 10., 7.,
10., 8., 8., 4., 5., 8., 4., 4., 5., 2., 4., 1., 1.,
0.])
Broadcasting
This is another really powerful feature of NumPy.
By default, array operations are element-by-element:
np.arange(5) * np.arange(5)
array([ 0, 1, 4, 9, 16])
If we multiply arrays with non-matching shapes we get an error:
np.arange(5) * np.arange(6)
ValueError Traceback (most recent call last)
<ipython-input-51-d87da4b8a218> in <module>()
----> 1 np.arange(5) * np.arange(6)
ValueError: operands could not be broadcast together with shapes (5,) (6,)
Or with a multi-dimensional array:
np.zeros([2,3]) * np.zeros([2,4])
ValueError Traceback (most recent call last)
<ipython-input-52-b6b30bdbcb53> in <module>()
----> 1 np.zeros([2,3]) * np.zeros([2,4])
ValueError: operands could not be broadcast together with shapes (2,3) (2,4)
Arrays must match in all dimensions in order to be compatible:
np.ones([3, 3]) * np.ones([3, 3]) # Note elementwise multiply, *not* matrix multiply.
array([[ 1., 1., 1.],
[ 1., 1., 1.],
[ 1., 1., 1.]])
Except, that if one array has any Dimension size of 1, then the data is automatically REPEATED to match the other dimension. This is known as broadcasting.
So, let’s consider a subset of our inflammation data (just so we can easily see what’s going on):
subset = data[:10, :10]
subset
array([[0., 0., 1., 3., 1., 2., 4., 7., 8., 3.],
[0., 1., 2., 1., 2., 1., 3., 2., 2., 6.],
[0., 1., 1., 3., 3., 2., 6., 2., 5., 9.],
[0., 0., 2., 0., 4., 2., 2., 1., 6., 7.],
[0., 1., 1., 3., 3., 1., 3., 5., 2., 4.],
[0., 0., 1., 2., 2., 4., 2., 1., 6., 4.],
[0., 0., 2., 2., 4., 2., 2., 5., 5., 8.],
[0., 0., 1., 2., 3., 1., 2., 3., 5., 3.],
[0., 0., 0., 3., 1., 5., 6., 5., 5., 8.],
[0., 1., 1., 2., 1., 3., 5., 3., 5., 8.]])
Let’s assume we wanted to multiply each of the 10 individual day values in a patient row for every patient, by contents of the following array:
multiplier = np.arange(1, 10)
multipler
array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
So, the first day value in a patient row is multiplied by 1, the second day by 2, the third day by 3, etc.
We can just do:
subset * multiplier
array([[ 0., 0., 3., 12., 5., 12., 28., 56., 72., 30.],
[ 0., 2., 6., 4., 10., 6., 21., 16., 18., 60.],
[ 0., 2., 3., 12., 15., 12., 42., 16., 45., 90.],
[ 0., 0., 6., 0., 20., 12., 14., 8., 54., 70.],
[ 0., 2., 3., 12., 15., 6., 21., 40., 18., 40.],
[ 0., 0., 3., 8., 10., 24., 14., 8., 54., 40.],
[ 0., 0., 6., 8., 20., 12., 14., 40., 45., 80.],
[ 0., 0., 3., 8., 15., 6., 14., 24., 45., 30.],
[ 0., 0., 0., 12., 5., 30., 42., 40., 45., 80.],
[ 0., 2., 3., 8., 5., 18., 35., 24., 45., 80.]])
Which gives us what we want, since each value in multiplier is applied successively to each value in a patient’s row, but over every patient’s row. So, every patient’s first value is multiplied by 1, every patient’s second value is multiplied by 2, etc.
Since multiplier has only one dimension, but the size of that dimension matches our number of days (the second dimension of subset), broadcasting automatically repeats the data in multiplier to match the number of patients (the first dimension in subset) so the * operation can be applied over arrays of equal shape.
Key Points
Processing NumPy arrays is generally much faster than processing Python lists.
NumPy arrays have specialised capabilities to support complex mathematical operations, and are less flexible that Python lists.
Slicing NumPy arrays returns a reference to the original dataset, not a copy of it like with Python lists.
NumPy arrays only hold elements of a single data type and are generally fixed in size.
Use
numpy.mean(array),numpy.max(array), andnumpy.min(array)to calculate simple statistics.Use
numpy.mean(array, axis=0)ornumpy.mean(array, axis=1)to calculate statistics across the specified axis.Use
.reshape()to resize a NumPy array to a different set of dimensions.Broadcasting allows you to apply an operation to two arrays of different shape, repeating the data in an array of a one-long dimension to match the larger array.